내일 5프로 오를주식
MDD 견딜 수 있을 만큼만 리스크 PART TWO 본문

주식을 잘 몰라도 인터넷에서 한번쯤은 봤을만한 유명한 짤이죠. 그림의 내용은 일반적인 투자자가 생각하는 장기투자자의 머릿속 생각이라면 실제는 아주 험난하다라는 비유를 나타내는 삽화인데, 사실 이 그림의 진짜 의미는 MDD에 있습니다.
MDD(Maximum Drawown: 고점 대비 최대 손실폭)란 주가 고점대비 최대하락까지 얼마만큼 하락하는지를 나타내는 것인데 사실 전 얼마전까지도 모르는 용어 였습니다. 하지만 용어만 모를뿐이지 주식경험이 있는 사람은 모두가 아는 의미이죠. 그런데 이게 왜 중요하냐면 아무도 MDD가 어디까지 인지 모른다는게 진짜 어려운거죠.
그런 의미에서 투자자들은 MDD를 회피하기 위해 가장 고전적이면서도 가장 강력한 방법인 분할 매수를 하는 겁니다. 또는 저의 용어로 견딜만큼만 매수하는 거죠. 그런데 제가 실제 투자하면서 항상 간지럽고 궁금하고 뭔가 말할수 없는 막막함이, 도대체 왜 분할 매수를 하는지 원리적으로 명쾌하기 설명하기 어려웠습니다. 하지만 사경인이라는 스타 강사가 나타나면서 저에게 큰 깨닳음을 주었습니다. 그의 강의를 듣고 제가 나름대로 소화해서 이 원리에 대해서 우리가 곰곰히 씹어서 소화해 봐야할 중요한 진리라고 생각해 이렇게 소개합니다.
* 약간의 수학적 계산이 필요하니 인내를 가지고 꼭 따라오시기 바랍니다. 이걸 이해하지 못하면 어쩔땐 왜 주식상담하면서 손절로 시작하는지, 왜 아무것도 하지마라고 하는지, 왜 받아가면서 매수하라고 하는지 이해할 수 없습니다.
산술평균 ≧조화평균

다들 이거 기억하시나요? 핵심은 조화평균은 절대로 산술평균을 넘어 설수 없다는 것인데요. 사실 중학교 수준의 수학이긴 하지만 이걸 어디까지 설명을 해야 할지 고민은 많이 됩니다. 그럼에도 실전에서 반드시 이해하고 넘어가야 해서 괴롭지만 인내하시고 좀더 직관적으로 예를 들어 봅시다.
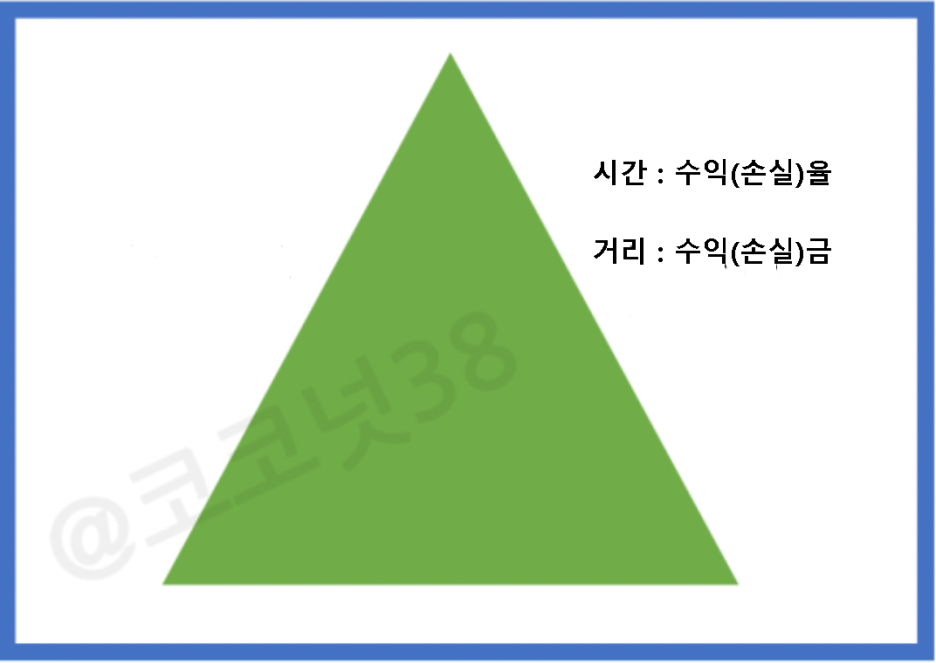
산술평균은 평지를 왔다갔다하는데 걸린시간의 평균이라고 생각하면되고 조화평균은 산을 넘어서 가는거라고 생각하면 됩니다. 그냥 상식적인 차원에서 산을 올라갈때는 힘드니까 천천히 갈테니 올라가는데 시간이 좀더 걸릴테고 내려갈때는 좀더 편하게 내려 올테니 시간이 덜 걸릴테죠. 그렇다면 만약 똑같은 거리를 간다고 했을때 평지를 왔다갔다 하는게 시간이 덜 걸리까요 아니면 산을 올라갔다 오는게 시간이 더 걸릴까요?
이것은 사실 수학을 몰라도 누구나 당연히 평지라고 생각할테지만 이게 주식으로 치환해보면 다들 아리송할겁니다. 좀더 구체적으로 생각해보면 시간을 주식에서 수익률(손실율), 거리를 수익(손실금)생각해 보면 조금더 직관적으로 이해하기 쉬울것 같습니다. 내려올때는 속도가 빠르기 때문에 시간(손실율)이 조금밖에 지나지 않았는데도 많은 거리 즉 많은 손실이 발생합니다. 하지만 반대로 올라갈때는 속도가 느리기 때문에 시간(수익율)이 많이 지나도 적은 거리 즉 적은 수익이 발생합니다.
더이상 나가면 아마도 머리가 뽀개질것 같습니다. 이번주엔 이것을 곰곰히 생각해 보고 다음주 세번째 편에, 실제 매매에서 이걸 어떻게 응용해서 견딜만큼만 매수하는지 정리해 봅시다.
* 사실 수학적으로 설명하면 아주 명쾌하게 해석이 되지만 그걸 이해하기에 다소 어렵다고 생각되서 비유적으로 하니 다소 수학적인 해석에 갭이 있습니다 하지만 우리는 모로가도 실전에서 응용만 하면 되지 않겠습니까? 아마도 3번째 이야기에서는 좀더 구체적인 적용이 있을 거라고 봅니다.
'개존다르의 생각' 카테고리의 다른 글
| 어뷰징 과 주식 이야기 ( 애드포스트 ) (2) | 2023.09.30 |
|---|---|
| 배드민턴과 주식 네 번째 이야기 (스플릿 스텝) (0) | 2023.09.30 |
| 배드민턴과 주식 세 번째 이야기(레슨받으면 더 안돼) (0) | 2023.09.29 |
| 분할매수 주식인은 긍정적 이어야 합니다. PART TWO (0) | 2023.09.29 |
| 배드민턴과 주식 두 번째 이야기 (쫙 펴고 풀스윙) (0) | 2023.09.29 |




